如何利用Python从头到尾的构建自己的卷积神经网络

什么是神经网络？

神经网络的大多数介绍性文字在描述它们时都会提起大脑类比。在不深入研究大脑类比的情况下，我发现将神经网络简单描述为将给定输入映射到所需输出的数学函数会更容易。

神经网络包含以下组件

• 一个输入层，X
• 任意数量的隐藏层
• 的输出层，ŷ
• 每个图层W和b之间的一组权重和偏差
• 每个隐藏层σ的激活函数的选择。在本教程中，我们将使用Sigmoid激活函数。

下图显示了2层神经网络的体系结构（请注意，在计算神经网络的层数时，通常不包括输入层）

在Python中创建神经网络类很容易。

训练神经网络

输出ŷ一个简单的2层的神经网络是：

您可能会注意到，在上式中，权重W和偏差b是影响输出ŷ的唯一变量。

自然，权重和偏差的正确值决定了预测的强度。根据输入数据微调权重和偏差的过程称为训练神经网络。

培训过程的每个迭代都包含以下步骤：

• 计算预测输出ŷ，称为前馈
• 更新权重和偏差，称为反向传播

下面的顺序图说明了该过程。

前馈

正如我们在上面的序列图中所看到的，前馈只是简单的演算，对于基本的2层神经网络，神经网络的输出为：

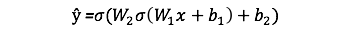
让我们在python代码中添加一个前馈功能即可做到这一点。请注意，为简单起见，我们假设偏差为0。

但是，我们仍然需要一种方法来评估我们的预测的“良好”（即，我们的预测有多远）？该损失函数允许我们这样做。

损失函数

有许多可用的损失函数，而问题的性质应决定我们对损失函数的选择。在本教程中，我们将使用简单的平方和错误作为损失函数。

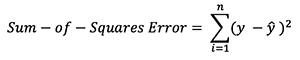
即，平方和误差仅是每个预测值与实际值之间的差之和。差异的平方，以便我们测量差异的绝对值。

我们训练的目标是找到使损失函数最小的最佳权重和偏差。

反向传播

现在，我们已经测量了预测的误差（损失），我们需要找到一种方法将误差传播回来，并更新权重和偏差。

为了知道适当的量来调整权重和偏差，我们需要知道损失函数相对于权重和偏差的导数。

从微积分回想起，函数的导数只是函数的斜率。

如果我们有导数，我们可以简单地通过增加/减少它来更新权重和偏差（请参见上图）。这就是所谓的梯度下降。

但是，由于损失函数的方程式不包含权重和偏差，因此我们无法直接计算损失函数相对于权重和偏差的导数。因此，我们需要链式规则来帮助我们进行计算。

！这很丑陋，但是它使我们能够获得所需的值–损失函数相对于权重的导数（斜率），以便我们可以相应地调整权重。

现在我们有了，让我们将反向传播功能添加到我们的python代码中。

为了更深入地了解微积分和链规则在反向传播中的应用，我强烈建议3Blue1Brown推荐本教程。

放在一起

现在，我们已经有了用于执行前馈和反向传播的完整python代码，让我们将神经网络应用于示例，看看它的效果如何。

我们的神经网络应该学习代表此功能的理想权重集。请注意，仅通过检查就可以算出重量并不是完全简单的事情。

让我们训练神经网络进行1500次迭代，看看会发生什么。查看下面的每次迭代损失图，我们可以清楚地看到损失单调地向最小值减小。这与我们之前讨论的梯度下降算法是一致的。

让我们看一下1500次迭代后神经网络的最终预测（输出）。

我们做到了！我们的前馈和反向传播算法成功地训练了神经网络，并且预测收敛于真实值。

请注意，预测值与实际值之间存在细微差异。这是理想的，因为它可以防止过度拟合，并使神经网络可以更好地概括未见数据。

下一步是什么？

对我们来说幸运的是，我们的旅程还没有结束。关于神经网络和深度学习还有很多东西要学习。例如：

• 除了Sigmoid函数外，我们还可以使用其他哪些激活函数？
• 训练神经网络时使用学习率
• 使用卷积进行图像分类任务

我很快会在这些主题上写更多的文章，所以一定要在Medium上关注我，并留意它们！

最后的想法

从头开始，我们当然已经学到了很多有关编写自己的神经网络的知识。

尽管诸如TensorFlow和Keras之类的深度学习库使在不完全了解神经网络的内部工作原理的情况下轻松构建深层网络，但我发现对于有抱负的数据科学家加深对神经网络的了解是有益的。